Introduction: Hello there maths lovers, in this post today you all will learn about the trigonometry and its definition along with angles, its types and different measurement systems. Please feel free comment your suggestions and questions down in the comments below. Happy Maths to You.
Trigonometry: The word trigonometry is taken from Greek words ‘trigon’ and ‘metron’ and the meaning for the words is ‘measuring the sides of a triangle’. Therefore trigonometry deals with the study of the measurement of triangles. The subject was originally created to solve geometric problems related to triangles. It was studied by sea captains for navigation, engineers and by surveyor to map out the new lands. But today its scope has been widened to a great extent and now it also includes the study of polygon and circle. Currently, it is used in many ares such as the science of seismology, describing state of atom, designing electric circuits, predicting height of tides in the ocean, analyzing a musical tone and in many other areas.
Angle in Geometry: Consider a line extending indefinitely in both directions. A point ‘O’ is dividing the line into two parts. The part of the line on one side of the point O is called a ray or half-line. Thus O divides the line into two rays OA and OA’.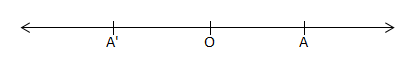
The point O is called vertex or origin of each of these rays. An angle is a figure formed by two rays having common vertex (origin). The rays are called sides of the angle.
An angle is denoted by the symbol ‘’ and it is followed by three capital letters, of which one in the middle denotes the vertex or origin of the angle and two other are points on the sides. It can also be simply denoted by one capital letter for vertex.
Example: The following figure is of an angle which is represented as .
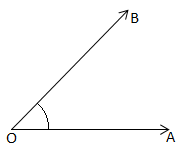
With each angle a number is associated and this number is called measure of the angle.
In geometry an angle always measure between and
and negative measurements doesn’t count. Measure of an angle is taken to be the smallest amount of rotation from the direction of one ray of the angle to the direction of the other ray.
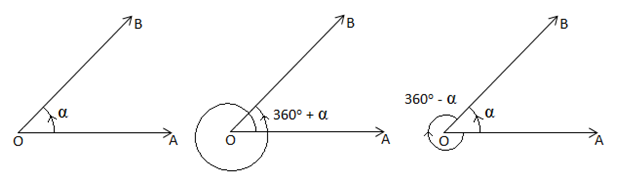
Angle in Trigonometry: In trigonometry idea of angle is different from the concept of angle in Geometry and it can be positive or negative as well and of any magnitude.
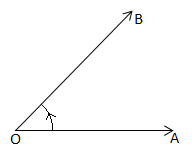
As in case of geometry, in trigonometry also the measure of the angle is the amount of rotation from the direction of one ray of the angle to the other. The initial and final positions of the revolving ray are respectively called the initial side (arm) and terminal side (arm) and the revolving line is called the generating line or the radius vector.
For example, if OA and OB be the initial and final positions of the revolving ray then angle formed will be .
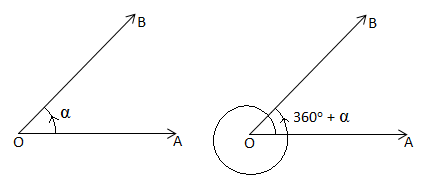
 Angles exceeding 360°: In geometry we measure angles from
Angles exceeding 360°: In geometry we measure angles from to
. But same is not the case in trigonometry because here rotation involves more than one revolution, for example, the rotation of a flywheel. In trigonometry we have the concept of angles greater than
. These angles can be formed in the following way:
The revolving line (radius vector) starts from the initial position and makes n complete revolutions in anticlockwise direction and also a further angle α in the same direction. We then have a certain angle
given by
Where and n is a positive integer or zero.
Thus there are infinitely many angles with initial side
and final side
.
For example, ,
, etc.
Sign of Angles: Angles which are formed by anticlockwise rotation of the radius vector are taken as positive whereas angles formed by clockwise rotation of the radius vector are taken to be as negative.
 Quadrants: Let XOX’ and YOY’ be two mutually perpendicular lines in a plane and OX be initial half line. The whole plane is divided into 4 different parts or regions as XOY, YOX’, X’OY’ and Y’OX. These regions are called quadrants and are respectively called 1st, 2nd, 3rd and 4th quadrant. The angle is said to lie in 1st, 2nd, 3rd and 4th quadrant according as the terminal side coincides with one of the axes, then angle is called a quadrant angle.
Quadrants: Let XOX’ and YOY’ be two mutually perpendicular lines in a plane and OX be initial half line. The whole plane is divided into 4 different parts or regions as XOY, YOX’, X’OY’ and Y’OX. These regions are called quadrants and are respectively called 1st, 2nd, 3rd and 4th quadrant. The angle is said to lie in 1st, 2nd, 3rd and 4th quadrant according as the terminal side coincides with one of the axes, then angle is called a quadrant angle.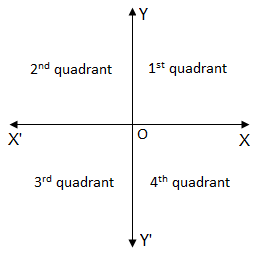 For any angle ‘
For any angle ‘’ which is not a quadrant angle and when number of revolution is not more than one and radius vector rotates in anticlockwise direction.
; if
lies in the 1st quadrant
; if
lies in the 2nd quadrant
; if
lies in the 3rd quadrant
; if
lies in the 4th quadrant
- when terminal side coincides with OY, angle formed =
- when terminal side coincides with OX’, angle formed =
- when terminal side coincides with OY’, angle formed =
- when terminal side coincides with OX, angle formed =
Unit of measurement of angles: In geometry angles are measured in terms of right angle. But in order to measure smaller angle we introduce smaller unit of angle.
There are three systems of units for the measurement of angles:
- Sexagesimal system
- Centesimal system
- Radian or circular measure
1. Sexagesimal or British System:
In this system of measurement a right angle is divided into 90 equal parts called Degrees. Each degree is then further divided into 60 equal parts called Minutes and each minute is again divided into 60 equal parts called Seconds.
A degree, a minute and second are respectively denoted by the symbols ,
and
.
Generally this system for the measurement of angles is most commonly used but it is not a convenient system of multipliers 90 and 60.
2. Centesimal or French System:
In this system of measurement a right angle is divided into 100 equal parts called Grades. Each grade is then divided into 100 equal parts called Minutes and each minute is further divided into 100 equal parts called Seconds.
A grade is denoted as , but symbol to denote minute and second are same, i.e.
and
.
Note: of centesimal system
of sexagesimal system
of centesimal system
of sexagesimal system
3. Radian or Circular Measure:
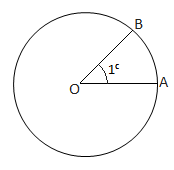
The angle subtended at the center by an arc of circle whose length is equal to the radius of the circle is called a radian and is denoted by .
We shall show that this angle is independent of the radius of the circle considered.
Let O be the center of a circle of radius r and let the length of arc AB = r
Then by the definition of radian
Examples:
Working Rule-
(ii) If the measure of an angle in degree and radian be D, G and C respectively, then
Ex. – 1. Express in
(i) Centesimal Measure, (ii) Radian Measure (take = 3.1415)
Ex. – 2. Express 1.2 radian in degree measure.
Sol. –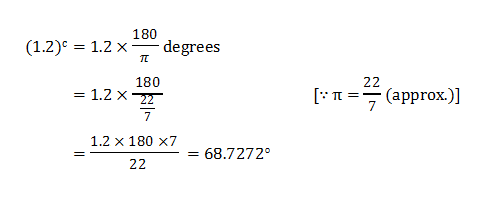
Ex. – 3. The angle of a triangle are in the ratio , find the smallest angle in degree and the greatest angle in radians.
Sol. – 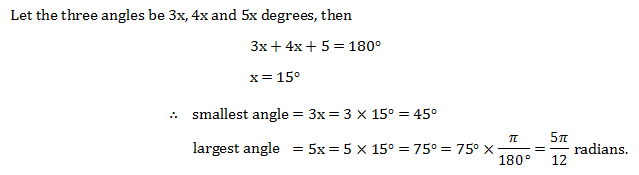
Exercises:
- Express
in centesimal measure.
- Express
in circular measure.
- Express
in sexagesimal measure.
- Two angles of a triangle are
and
respectively. Find the third angle in radians.
- The angles of a triangle are in A. P. and the number of radians in the greatest angle is to the number of degrees in the least one as
; find the angles in degree.
- The angles of a triangle are in A. P. and the number of grades in the least is to the number of radians in the greatest is
; find the angles in degree.
- Three angles are in G. P. The number of grades in the greatest angle is to the number of circular units in the least as 800 to
, and the sum of the three angles is
. Find the angles in grade.
- Find the angle between the hour-hand and minute-hand in circular measure at 4 O’ clock.
- Express in sexagesimal system of angular measurement the angle between the minute-hand and the hour-hand of a clock at quarter to twelve.
P.S. – Find your Answers here.
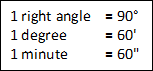
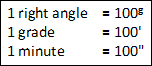
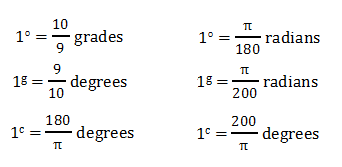


if solutions are available then send me.
Amazing experience …