A right angled triangle is a triangle where one of the internal angles is 90°.
Consider the general right angle triangle, in figure 1 below, with angle β and sides labeled as shown below
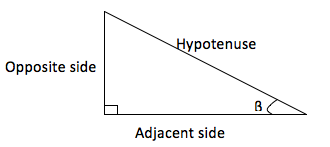
The sides are labeled with respect to the angle β, so that the nearest side is called the adjacent side, the side that is directly opposite is called the opposite side while the longest side is called the hypotenuse.
Therefore, given any angle in a triangle, it should be easy to identify the adjacent, the opposite side and the hypotenuse.
Example
Reference to the figure below.
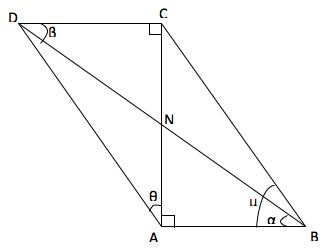
1. Identify the right angle triangles in the above diagram.
Solution: A right angled triangle is a triangle where one of the internal angles is 90°. Such triangles are ABC, ABN, DAC and DNC.
2. Identify the adjacent sides to angles θ, α, β and µ.
Solution:
- Angle θ is in triangle DAC. The angle is nearer to line AC hence, it is the adjacent line.
- Angle α is in triangle ABN. The angle is nearer to line AB hence, it is the adjacent line.
- Angle β is in triangle DNC. The angle is nearer to line DC hence, it is the adjacent line.
- Angle µ is in triangle ABC. The angle is nearer to line AB hence, it is the adjacent line.
3. Identify the opposite sides to angles θ, α, β and µ.
Solution:
- Angle θ is in triangle DAC. The angle is opposite to line DC hence, it is the opposite line.
- Angle α is in triangle ABN. The angle is opposite to line AN hence, it is the opposite line.
- Angle β is in triangle DNC. The angle is opposite to line CN hence, it is the opposite line.
- Angle µ is in triangle ABC. The angle is opposite to line AC hence, it is the opposite line.
4. Identify hypotenuse with respect to angles θ, α, β and µ.
Solution:
- Angle θ is in triangle DAC. The longest side in that angle triangle is AD hence, it is the hypotenuse.
- Angle α is in triangle ABN. The longest side in that angle triangle is NB hence, it is the hypotenuse.
- Angle β is in triangle DNC. The longest side in that angle triangle is DN hence, it is the hypotenuse.
- Angle µ is in triangle ABC. The longest side in that angle triangle is CB hence, it is the hypotenuse.
We will cover the following. Feel free to skip any section as you prefer.
- Trigonometric ratios
- Relationship between cosine, sine and tangent
- Trigonometric ratio of a complement
- Area of a triangle
Trigonometric ratios
Let us consider the below right angle triangles, with the measurements stated as follows.
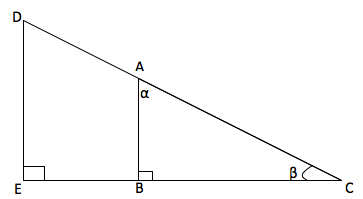
Let AB = 3cm, BC = 4cm, AC = 5cm, ED = 3.75cm, EC = 5cm and DC = 6.25cm
Consider the following ratios in triangles ABC and ECD
In triangle ABC,
,
,
In triangle DEC,
,
,
It can be seen that the corresponding ratios are equal.
,
,
This property makes them have special names. These ratios with respect to a specific angle, say β, are called trigonometric ratios.
For instance, with reference to
The fraction of opposite side over adjacent side is called tangent (abbreviated as tan), the fraction of adjacent side over hypotenuse is called Cosine (abbreviated as cos) and the fraction of opposite side over hypotenuse is called Sine (abbreviated as sin).
Therefore
If we adopt the following symbols, Adjacent side (A), Opposite side (O) and Hypotenuse (H), then we have the following ,
and
. Using this notation, we have an easier way of memorizing, that is, SOHCAHTOA.
- SOH = Sin is Opp Side Over Hypotenuse
- CAH = Cos is Adj Side Over Hypotenuse
- TOA = Tan is Opp Side Over Adj Side
Note that when α and β (any two angles) are not equal, then there trigonometric ratios are not necessarily equal.
Examples
1. Find the sine, cosine and tangent of the α and β using the figure below
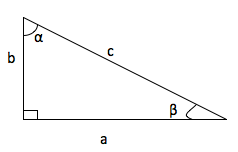
Solution:
sine, cosine and tangent of α
Using SOHCAHTOA,
We have
sine, cosine and tangent of β
Relationship between cosine, sine and tangent
We have seen that
Examples
1. Find the tangent of an angle if its sine and cosine is 0.2 and 0.05 respectively.
Solution: From the relationship of sin, cos and tan, we have
2. The hypotenuse, PQ, of a triangle is PQR is 25 inches. If the base, PR, is 24 inches, find the value of tan c and cos b where c and b are angles PQR and angles QPR respectively.
Solution:
We make a sketch to represent the information. Since, PQ is the hypotenuse and the right angle is usually opposite to the hypotenuse, the angle PRQ must be the right angle.
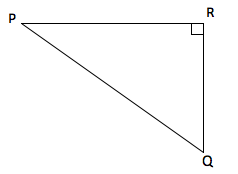
We use Pythagorean Theorem to find the height, RQ, of the triangle. By Pythagorean Theorem
Upon substitution, we have
3. If , find the value of tan h and cos h + sin h.
Solution:
Since we apply the formula
Therefore, the opposite side is 3 units while the hypotenuse side is 7 units. The appropriate diagram is as shown below.
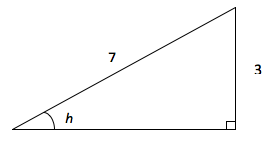
Using Pythagorean Theorem, we have;
Upon substitution, we have
Upon substitution, we have
Adj =
cos h + sin h = 0.9036 + 0.4286 = 1.3322.
Trigonometric ratio of a complement
Complement angles add up to 90°. Therefore, a complement of an angle say, h, is 90° – h.
Consider the following diagram.
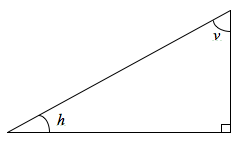
Since interior angles of a right angle add up to 180, and one of the angles is a right angle, we have
h + v + 90 = 180. Writing v in terms of h, we have v = 180 – 90 – h = 90 – h Thus, v = 90 − h
To show that v and h are complementary angles, we add the two v + h = 90 – h + h = 90°.
Therefore, v and h are complementary angles.
Examples
1. Given that , find the value of sin (90 – x) and cos (90 – x).
Solution:
implies that the adjacent side of the triangle is 4 units while the hypotenuse is 7 units.
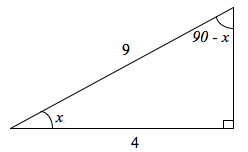
We determine the opposite side using the Pythagorean Theorem. Thus, the
Opposite side
The opposite of 90 – x is equal to 4 units, its adjacent side is equal to 8.062 units while the hypotenuse is 8.062.
Thus,
2. If t+p = 90°, find that value of tan t – sin t and cos t if tan p = 2.4.
Solution:
Since Opposite side = 12 units and Hypotenuse = 5 units. The diagrammatic representation is as shown below.
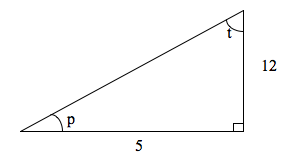
Using the Pythagorean Theorem, we have compute the hypotenuse as;
H = 13
So
Area of a triangle
The area of a general triangle, in most cases, is given in terms of the product of two lines and an angle that lies between the two lines. Note that the area of a triangle is generally given as;
By height, we mean the perpendicular height.
Consider the following triangle whose direct height is not given. Assume that only the value of p, q and θ are given and you are required to determine the area of the triangle.

We can express h in terms of p and θ. Remember that with reference to angle θ, p is the hypotenuse and h is the opposite side, we can apply the sine ratio.
Multiplying through by p, we have h = p sin θ
Substituting into the equation for the area of the triangle, we have
Area of triangle = =
In general, the area of a triangle given two sides and an angle between the two sides is half the product of the sides and the sine of the angle between them.
Note that when the angle between the two lines is 90°, we have the right angle triangle. Since sin 90° = 1 (to be covered in the following articles), the formula, area = 1/2 pq still remains valid.
Examples
Determine the area of a triangle given that the two sides are 8 inches and 10 inches respectively where the lines intersect at an angle of 30°.
The sides that intersects at 30° measures 8 inches and 10 inches respectively, therefore from above, the area is given by , upon substitution, we have
Area = square inches.
Exercise
Use the following diagram to answer questions 1 and 2.
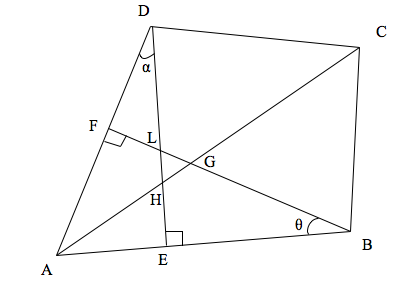
1. How many right angle triangles can be identified in the diagram? Name them.
2. Identify all possible hypotenuse, adjacent and opposite sides of angles θ and α.
3. Find the sine of angle ABC if angle CAB is a right angle, AB = 60 units, CB = 61 units.
4. Find the area of a triangle ABC if angle CAB is a right angle, AB = 8 units, CB = 10 units.
5. The area of a triangle is 6 square inches. If the triangle has two sides measuring 4 inches and x inches respectively that intersect at 30°. Find the value of x.
6. Determine the value of the following given that
Write your answers in fraction form.
7. A ladder is inclined to the wall of the building at an angle of 60°. If the ladder is 5 feet long, how high is the point of contact of the ladder to the wall from the foot of the wall? (Write your answer to the nearest unit)
8. The tangent of an angle is 0.6, if its sine is 0.2, find its cosine. Write your answer correct to two decimal places.
9. A triangle PQL is such that its base PQ = 8 inches and QL = 5 inches. If the size of angle LPQ is half the right angle, find the area of the triangle.
10. A person standing on a level ground realizes an airplane at angle of 50°. If the airplane is 1.5 miles above, how far is the person from the point on the ground that is directly below the plane?
Leave a Reply