Understanding the Concept of Limits

We know division by zero is not possible in mathematics. If we consider the function definition as

$f(x)=\dfrac{(x^{2}-1)}{(x-1)}$

The value of f(x) at x=1 is indeterminate.

$f(1)=\dfrac{(1^{2}-1)}{(1-1)} = \dfrac 0 0$

More simply, the value of the function f(x) does not exist at x=1. So, instead of x=1 we consider values of x sufficiently close to 1, i.e., as close to 1 as possible.

x	f(x)
0.5	1.50000
0.9	1.90000
0.99	1.99000
0.999	1.99900
0.9999	1.99990
0.99999	1.99999
…	…

From the table above we can see that as the values of x approach 1, the value of the function f(x) approach 2. In the table we have stopped at 0.99999, but if we take values of x even closer to 1, the corresponding values of f(x) will be even closer to 2. Here, as the values of x increase towards 1 the values of f(x) increase towards 2. This is symbolically written as:

$\lim\limits_{x \to 1+} f(x) = 2$

It reads, “limit x tends to 1 plus f(x) is equal to 2”. It is to be noted that the ‘+’ sign signifies values of x greater than 1 and not “positive” values of x.

Let us now look at the following table

x	f(x)
1.5	2.50000
1.1	2.10000
1.01	2.01000
1.001	2.00100
1.0001	2.00010
1.00001	2.00001
…	…

Again from the above table we can see that as the values of x come closer and closer to 1, the corresponding values of f(x) come closer and closer to 2. In other words, as the values of x approach 1, the corresponding values of f(x) approach 2. The only difference is that here the values of x decrease towards 1 and the values of f(x) decrease towards 2. This is symbolically written as:

$\lim\limits_{x \to 1-} f(x) = 2$

It reads, “limit x tends to 1 minus f(x) is equal to 2”. It is to be noted that the ‘-‘ sign signifies values of x less than 1 and not “negative” values of x.

In practice, the numerical difference between the value x=1 and a value of x sufficiently close to 1 (such as, x=1.0000001 or x=0.9999999) can me made as small as we please and hence can be neglected. Similarly, the numerical difference between the value f(x)=2 and a value of f(x) very close to 2 can be made as small as we please and hence be neglected if the value of x is taken sufficiently close to 1.

In general, when the value of f(x) cannot be determined for a particular value of x, say, x=a then there may exist a definite finite number b, such that the value of f(x) gradually tends to that finite number b when x tends to a. However we cannot say whether that finite number b will always exist or not. From this observation, the concept of limit has been developed by mathematicians.

Limit of a Variable

Let us consider a real variable x. Let a be a constant. Then by ‘x tends to a’ we mean x successively assumes values either greater than or less than a and the numerical difference between the assumed value of x, i.e., |x-a| becomes smaller and smaller. In this case, x becomes very close to a (but x≠a) and we say ‘x approaches a’.

If x approaches a assuming values greater than a then we say ‘x tends to a from the right side’ and we denote it by $x \to a^+$ .

If x approaches a assuming values less than a then we say ‘x tends to a from the left side’ and we denote it by $x \to a^-$ .

Limiting Value of a Function

We assume x to be a real variable, a is a real constant and f(x) is a single-valued function of x.

If x gradually approaches a assuming values which are greater than a and if the corresponding values of f(x) exist and these values gradually approach a finite constant $l_1$ , then $latexl_1$ is called the right hand limiting value of f(x) or the right hand limit of f(x) and it is denoted by,

$\lim\limits_{x \to a+} f(x) = l_1$

Again, if x gradually approaches a assuming values which are less than a and if the corresponding values of f(x) exist and these values gradually approach a finite constant $latexl_2$, then $latexl_2$ is called the left hand limiting value of f(x) or the left hand limit of f(x) and it is denoted by,

$\lim\limits_{x \to a-} f(x) = l_2$

When x approaches a assuming values either greater than or less than a and f(x) assumes finite values for every value of x and if those values of f(x) gradually approach a finite constant l, then l is called the limiting value of f(x). It is denoted by,

$\lim\limits_{x \to a} f(x) = l$

The limit of the function $l = \lim\limits_{x \to a} f(x)$ exists only if both $l_1$ (the right hand limit) and $l_2$ (the left hand limit) exist and $l_1=l_2$ , i.e., if

$\lim\limits_{x \to a+} f(x) = \lim\limits_{x \to a-} f(x)$

l does not exist if,

$l_1$ is indeterminate OR
$l_2$ is indeterminate OR
$l_1 \neq l_2$ .

What do we mean by 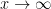$x \to \infty$ and $x \to-\infty$ ?

If a real variable x assumes positive values and increases without limit, taking up values larger than any large number one can imagine, then we say that the variable x tends to infinity in the positive direction and denote it by $x \to \infty$ .

If a real variable x assumes negative values and increases numerically without limit, taking up values which are numerically larger than any large number one can imagine, then we say that the variable x tends to infinity in the negative direction and denote it by $x \to-\infty$ .

Some Important Limits

1. If n is a rational number, then $\lim\limits_{x \to a} \dfrac{x^n-a^n}{x-a} = n . a^{n-1}$

2. If n is a rational number, then $\lim\limits_{x \to 0} \dfrac{(1+x)^n-1}{x} = n$

3. $\lim\limits_{x \to 0} \dfrac{sin x}{x} = 1$

4. $\lim\limits_{x \to 0} \dfrac{e^x -1}{x} = 1$

5. $\lim\limits_{x \to 0} {(1+x)}^{\dfrac {1}{x}} = e$

6. $\lim\limits_{x \to 0} \dfrac{a^x -1}{x} = ln a [a>0]$

7. $\lim\limits_{x \to \infty} {(1+\dfrac{1}{x})}^x = e$

Points to Remember

$x \to 0^+$ does not mean that x takes positive values. It means that x approaches 0 assuming values greater than 0.
$x \to 0^-$ does not mean that x takes negative values. It means that x approaches 0 assuming values less than 0.
$\lim\limits_{x \to a+} f(x)$ is called the right hand limit of f(x) at x=a and $\lim\limits_{x \to a-} f(x)$ is called the left hand limit of f(x) at x=a.
$\lim\limits_{x \to a} f(x)$ exists if $\lim\limits_{x \to a+} f(x)$ and $\lim\limits_{x \to a-} f(x)$ both exists and $\lim\limits_{x \to a+} f(x) = \lim\limits_{x \to a-} f(x)$
Limit of a function may not exist as and when the above conditions are not fulfilled. If not, the limit of the function at that point does not exist.

Questions and Answers

Question 1: Does $\lim\limits_{x \to 2} \dfrac{x^2-4}{x-2}$ exist? If so find its value?

Solution: Let $f(x) = \dfrac{x^2-4}{x-2}$

x	f(x)
1.9	3.9
1.99	3.99
1.999	3.999
1.9999	3.9999
…	…
2.1	4.1
2.01	.401
2.001	4.001
…	…

From the above table we can see that as x approaches the finite value 2 (assuming values either greater than or less than 2 and sufficiently close to 2) the values of f(x) gradually approach 4 and the difference between the values of f(x) and 4 can be made as small as we please. Hence, $f(x) \to 4$ as $x \to 2$ , but x≠2 because f(x) is undefined at x=2.

Left hand limit = $\lim\limits_{x \to 2-} f(x) = 4$
Right hand limit= $\lim\limits_{x \to 2+} f(x) = 4$

Clearly both Right hand limit and left hand limit exist and are equal.

Therefore, $\lim\limits_{x \to 2} \dfrac{x^2-4}{x-2}$ exists and $\lim\limits_{x \to 2} \dfrac{x^2-4}{x-2} = 4$

Question 2: Evaluate $\lim\limits_{x \to 1} \dfrac{1}{(x-1)^2}$

Solution: Let $f(x) = \dfrac{1}{(x-1)^2}^2$

x	f(x)
0.9	$10^2$
0.99	$10^4$
0.999	$10^6$
…	…
1.1	$10^2$
1.01	$10^4$
1.001	$10^6$
…	…

From the above table we can see that as x gradually approaches the finite value 1 from the left, assuming values less than 1, the value of f(x) keeps increasing and approaches a large number, as large as we can imagine.

Left hand limit = $\lim\limits_{x \to 1-} f(x) = +\infty$

Also, we can see that as x gradually approaches the finite value 1 from the right, assuming values greater than 1, the value of f(x) keeps increasing and approaches a large number, as large as we can imagine.

Right hand limit = $\lim\limits_{x \to 1+} f(x) = +\infty$

So left hand limit is equal to right hand limit. $\lim\limits_{x \to 1-} f(x) = \lim\limits_{x \to 1+} f(x) = +\infty$

Therefore, $\lim\limits_{x \to 1+} f(x) = \lim\limits_{x \to 1} \dfrac{1}{(x-1)^2} = +\infty$

NOTE: Here, x≠1 because at x=1, $f(x)=\dfrac {1}/{(1-1)^2} = \dfrac {1}{0}$ which is undefined.

Question 3: Evaluate $\lim\limits_{x \to 0} \dfrac{1}{x}$

Solution : Let $f(x) = \dfrac{1}{x}$

x	f(x)
-0.1	-10
-0.01	-100
-0.001	-1000
…	…
0.1	10
0.01	100
0.001	1000
0.0001	10000
…	…

From the above table we can see that $\lim\limits_{x \to 0-} f(x) = -\infty$ and $\lim\limits_{x \to 0+} f(x) = +\infty$

Clearly $\lim\limits_{x \to 0-} f(x) \neq \lim\limits_{x \to 0+} f(x)$ i.e., left hand limit and right hand limit exist, but they are not equal.

Therefore $\lim\limits_{x \to 0} \dfrac{1}{x}$ does not exists.

Question 4: Evaluate $\lim\limits_{x \to -\infty} (1 + \dfrac{2}{x^2})$ .

Solution : Let $f(x) = (1 + \dfrac{2}{x^2})$ .

x	f(x)
-10	-1.02
-100	-1.0002
-1000	-1.000002
-10000	1.00000002
…	…

From the table we can see that as x increases numerically without limit, assuming negative values, the numerical difference between f(x) and the finite value 1 can be made as small as we please. Hence, as $x \to -\infty , f(x) \to 1$ .

Therefore $\lim\limits_{x \to -\infty} f(x) = \lim\limits_{x \to -\infty} (1 + \dfrac{2}{x^2}) = 1$ .

Question 5: Evaluate

$\lim\limits_{x \to 2} (2x^2 - 3x + 5)$

$\lim\limits_{x \to 3} \dfrac {x^2-9}{x-3}$

Solutions:

$\lim\limits_{x \to 2} (2x^2 - 3x + 5)$

= $\lim\limits_{x \to 2} (2x^2) - \lim\limits_{x \to 2}3x + \lim\limits_{x \to 2}5$

= $2 \lim\limits_{x \to 2} (x^2) - 3\lim\limits_{x \to 2}x + 5$

= $2 (2^2) - 3\times2 + 5$

= 7

b. Let $f(x) = \dfrac {x^2-9}{x-3}$

Now $(x^2-9) = (x-3)(x+3)$

Therefore $f(x) = \lim\limits_{x \to 3} \dfrac {x^2-9}{x-3} = \lim\limits_{x \to 3} \dfrac {(x-3)(x+3)}{x-3}$

= $f(x) = \lim\limits_{x \to 3} (x+3)$

= 3 + 3 = 6

Exercise

1. Show that $f(x) = \lim\limits_{x \to -2} (\surd x^3 + 3x^2 - x + 3) = 3$

2. Evaluate $\lim\limits_{x \to 1} \dfrac{x^2-3x+2}{x^2-4x+3}$ . (Hint: factorize the numerator and the denominator)

3. Evaluate $\lim\limits_{x \to 1} \dfrac{x^2-5x+6}{x^2-5x+2}$ .

4. Show that $\lim\limits_{x \to -2} \dfrac{x^2-5x+3}{x^2+1}$ .

5. Evaluate $\lim\limits_{x \to 2} \dfrac{x - \surd 3(x-2)}{x^2-4}$ . [Hint: Multiply both the numerator and the denominator by ${x + \surd 3(x-2)}$ . and rationalize]