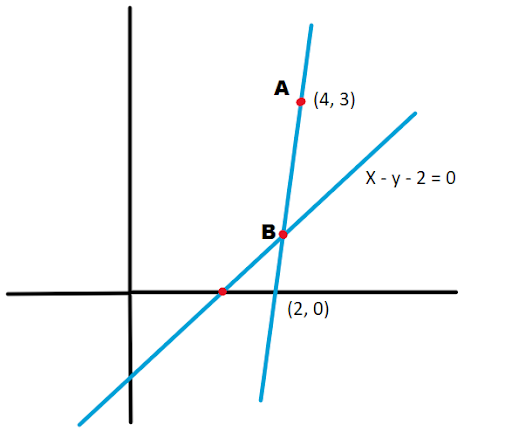
Line with slope greater than 1 passes A(4, 3) and intersects x–y=2 at B

A line with a slope greater than 1 passes through point A(4, 3) and intersects the line x – y – 2 = 0 at point B. If the length of the line segment AB is $\frac{{\sqrt {29} }}{3}$ , then B also lies on the line

2x + y = 9
3x – 2y = 7
x + 2y = 6
2x – 3y = 3

Solution:

Firstly make the graph according to the question.

Use the formula to find the length of the line segment.

Then identify which line satisfy point B.

Step 1 of 3:

According to the question, we get

Step 2 of 3:

We have A(4, 3)

Let B(a, b) = B(a, a-2)

Also, given that length of line segment AB = $\frac{{\sqrt {29} }}{3}$

But we know that,

If $A({x_1},{y_1})\& B({x_2},{y_2})$ then length $AB = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}}$

$\therefore AB = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {a - 2 - 3} \right)}^2}}$

$\Rightarrow \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {a - 2 - 3} \right)}^2}} = \frac{{\sqrt {29} }}{3}$

On squaring both sides

$\begin{gathered} \Rightarrow {\left( {a - 4} \right)^2} + {\left( {a - 5} \right)^2} = \frac{{29}}{9} \hfill \\ \Rightarrow \left( {{a^2} - 8a + 16} \right) + \left( {{a^2} - 10a + 25} \right) = \frac{{29}}{9} \hfill \\ \Rightarrow 2{a^2} - 18a + 41 = \frac{{29}}{9} \hfill \\ \Rightarrow 9\left( {2{a^2} - 18a + 41} \right) = 29 \hfill \\ \Rightarrow 18{a^2} - 162a + 369 = 29 \hfill \\ \Rightarrow 18{a^2} - 162a + 369 - 29 = 0 \hfill \\ \Rightarrow 18{a^2} - 162a + 340 = 0 \hfill \\ \Rightarrow 2(9{a^2} - 81a + 170) = 0 \hfill \\ \Rightarrow 9{a^2} - 81a + 170 = 0 \hfill \\ \Rightarrow {a^2} - \frac{{81}}{9}a + \frac{{170}}{9} = 0 \hfill \\ \end{gathered}$