The earlier chapter on Complex Numbers explained what we mean by a complex number together with a few properties of complex numbers. Basic mathematical operations of complex numbers were introduced. So, the previous chapter may be considered as the preliminary base on which this chapter aims to build further. In this chapter we shall cover a few advanced topics under complex numbers.
Amplitude(or Argument) of a complex number:
Let where
are real,
and
; then the value of
for which the equations:
…(1) and
…(2)
are simultaneously satisfied is called the Argument(or Amplitude) of and is denoted by
.
Clearly, equations (1) and (2) are satisfied for infinite values of ; any of these values of
is the value of
. However, the unique value of
lying in the interval
and satisfying equations (1) and (2) is called the principal value of
and we denote this principal value by
or
.Unless otherwise mentioned, by argument of a complex number we mean its principal value.
Since, and
(where n=any integer), it follows that,
where
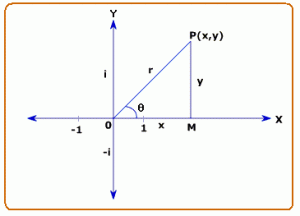
Geometrical representation of modulus and amplitude:
Let us assume that the point represents the complex number
. We draw perpendicular
on
and join
. If
and
, then from the right-angled triangle
we get,
and
where,
and
This form of representation, where,
and
of the complex number
, is called the polar form or the modulus-amplitude form of z.
If the point represents the complex number
and
then:
a) when P lies in the first quadrant
b) when P lies in the second quadrant
c) when P lies in the third quadrant
d) when P lies in the fourth quadrant
Note:
1) The horizontal axis or the -axis is also called the real axis. The vertical axis or the
-axis is called the imaginary axis.
In particular,
when P lies on the positive real axis, principal value of is 0.
when P lies on the negative real axis, principal value of is
.
when P lies on the positive imaginary axis, principal value of is
.
when P lies on the negative imaginary axis, principal value of is
.
2) The argument of i.e.,
i.e., the origin O, is not defined.
3) It must be kept in mind that is the principal value of
while
is just one of the many values of
which satisfy the equations,
…(1) and
…(2)
Example: Find the amplitude of
Solution:
Clearly, in the z-plane, the point lies in the second quadrant.
Hence, if then,
where,
the reqiured amplitude of
Example: Find the amplitude of
Solution:
Clearly, in the z-plane, the point lies in the fourth quadrant.
Hence, if then,
where,
, i.e., the required amplitude of z is
Algebra of Complex Numbers:
Let and
Now, in the earlier chapter “Complex Numbers” we have shown that:
For addition: where:
and
and both are real.
For subtraction: where:
A=a-c $ and and both are real.
For multiplication: where:
and
and both are real.
Note: Proceeding similarly, the product of more than two complex numbers can be expressed in the form
For division: where:
and
and both are real.
So, it is very clearly that when the four fundamental mathematical operations, viz., addition, subtraction, multiplication and division carried out between two complex numbers, the result is also a complex number of the form where both
and
are real.
Now, we consider two more algebraic operations:
1) Any integral power of a complex number is a complex number:
Let be a complex number where
are real and let
be any integer.
Case I: If is a positive integer then,
[ the product of more than two complex numbers can be expressed in the form
] where,
are real.
Case II: If is a negative integer w eassume
where m is taken to be any positive integer.
Then, where
are real.
where, and
any integral power of a complex number is a complex number.
2) Any root of a complex number is a complex number:
Let be a complex number where
are real and let
be any positive integer.
If the root of z be
then,
By hypothesis, Hence,
is an imaginary quantity.
Now, can be an imaginary quantity if and only if
is an imaginary number and equation (1) will be satisfies if and only if
is an imaginary number of the form
where
are real.
any root of a complex number is a complex number.
Properties of Complex Numbers:
1) If are real and
then
2) If are real and
then
and
3) The set of complex numbers satisfies commutative, associative and distributive laws, i.e., if be three complex numbers then,
i) [commutative law for addition] and
[commutative law for multiplication].
ii) [associative law for addition] and
[associative law for multiplication].
iii) [distributive law]
4) The sum and product two conjugate complex numbers are both real.
Proof: Let be a complex number where
are real.
Then, conjugate of
Now, which is real.
Again, which is real.
Note: If then,
Again,
Hence,
modulus of a complex quantity =the positive square root of the product of the complex quantity and its conjugate.
5) If the sum and product of two complex numbers are both real, then the complex numbers are conjugate to each other.
Proof: Let and
be two complex numbers where
are al real and
It is given that the sum of and
is real.
is real.
Also, is real.
[
]
[
]
which shows that
and
are conjugate to each other.
6) For two complex numbers and
,
Proof: Let and
and
Again,
Now,
Note:
1) For three complex numbers we have,
Proof:
In general, for n complex numbers we have,
2) For two complex numbers and
, we have,
i)
ii)
Proof:
i)
ii)
Similarly,
From (1) and (2) we get,
Exercise:
1) Express in the form where
are real:
2) Find the amplitude of the following complex numbers:
3) If and
, show that,
4) Express in modulus-amplitude form.
5) If
Good