Point
Point is the basic building block of Geometry. Every shape is made through the combining the points.
A small dot marked by a pencil is a point. A point has no length or width. It has no thickness. Point is a mark of position. A point specifies the exact location. Point is denoted by a dot (.) and is named by an alphabet.
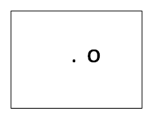
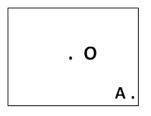
In the figure above, O is a point as it has a definite mark. Here it indicates this point O is located at the centre of the plane. In the figure below, there is another point A. It is located at right bottom of the plan.
Ray
Let us think of a torch. The light rays come out of it and move away. Let us take example of sun. The rays start from sun and go in all directions and reach to us.
In Geometry also, a ray starts from a point and may go to infinity. It has staring point but has no end point. We say a ray has one endpoint and goes without end in one direction.

In the figure above, the starts from A and the arrow denotes it can go to infinity.
Its length cannot be measured. An unlimited number of rays can be drawn in different directions from a given point
The rays coming from torch or sun are examples of rays.
This is a ray because a ray has one endpoint and goes without end in one direction
Line

Look at the figure above. There are arrows on both sides. It indicates it can go further on both sides without end. This is called line.
A line goes without end in both directions. Both ends of a line can go to infinity. A line has no end points. The length of a line cannot be measured. A line has no definite length.
A line is named by any two points on it and written as line AB or line PQ. One and only one line can be drawn passing through two given points A and B. This line is called AB. It may also be called BA. Line BA is the same as line AB. Both pass through the same two points A and B.
An unlimited number of lines can be drawn passing through a given point A.
A horizontal line goes straight left or right across. A vertical line goes straight up or down.
A diagonal line can be in any direction between horizontal line and vertical line.
Line Segment
![]()
Now look at the figure above. There is no arrow on any end. It starts from one point and ends at another point. This is called a line segment. A section of a line is a line segment.
A line segment has two endpoints. A line segment is a straight line that connects two points. It is the shortest path between the two points. A line segment has definite length. Its length can be measured.
Let us mark two small dots (.) by a pencil as points A and B. Let us join them by drawing a straight line. This forms a line segment. A line segment is named by its two endpoints and written as line-segment AB or line-segment PQ.
![]()
In the figure above, a line segment AB has two end points A and B. It starts from point A and ends at point B. One and only one line-segment can be between two given points A and B. This line-segment is called AB. It may also be called BA. Line BA is the same as line AB. Both pass through the same two points A and B.
Line segment can also be a part of a line as in the figure below.
![]()
A line-segment may be also a part of ray. In the figure below, a line segment AB has two end points A and B. It is a part of a ray starting from A.
![]()
Parallel lines
Two lines in the same plane either meet or do not meet. If the two lines on a plane meet, we say the two lines intersect and the point where they meet is called point of intersection. If the two lines cannot meet at any point, they are called parallel lines. No two points can be common to two parallel lines.
![]()
In the figure above, the two lines do not intersect each other. Even if we extend these lines further, they will not touch or meet each other. They are parallel lines.
Intersecting lines
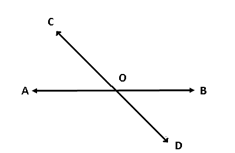
Let us look at the two lines AB and CD in figure above. They intersect at point O. Hence they are not parallel lines. Point O is the point of their intersection.
Concurrent lines
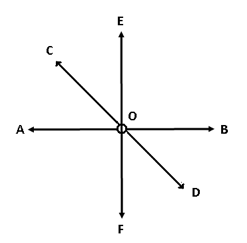
Three or more lines passing through the same point on a plane are called concurrent lines. In the figure below, the three lines AB, CD and EF intersect each other at point O.
Collinear points
Three or more points in a plane* are said to be collinear if they all lie on the same line.
![]()
In the figure above, points A, B and C are on the same line. Hence these three points A, B and C is collinear.
*Flat surface is called a plane in Geometry. We can say a piece of paper from our Exercise Book is a plane.
Measurement of line segment
A ruler is an instrument used in geometry. We use a ruler to draw a line segment. We use it also to measure length of a line segment.

A ruler is generally 1 ft (30 cm) long and is called One foot ruler. Sometime it is simply called scale. Some rulers are six inches (15cm) long and are called half foot ruler. One edge of a ruler has scales marked in inches and the other edge has scales marked in cm.
We place the ruler with its edge along the line-segment AB with the zero mark of the ruler at the start point A of the line-segment. We read the mark on the ruler at the other endpoint B of the line-segment.
Points to Remember
- A small dot marked is a point.
- A point has no length, width or thickness.
- A point specifies the exact location.
- A ray starts from a point and goes to infinity.
- A line has no end points.
- A line segment has two endpoints.
- A line segment connects both endpoints.
- If the two lines cannot meet at any point, they are called parallel lines.
- Three or more points on the same line are said to be collinear points
- A ruler is used to draw a line segment and measure its length.
Questions and Answers
Question 1: Draw two points A and B on a paper and draw line-segment.
Answer: We mark a Point A on a writing page and then mark another point B on the same Page. We join these two points using a line. This is the line segment.
![]()
Question 2: Draw two intersecting lines.
Answer: We take a ruler and draw a line AB. Then we slightly turn the ruler and draw another line CD in such a way that it passes through any one point of line AB.

Question 3: Write two main differences between line and line segment.
Answer:
- A line segment has two endpoints. A line has no end point.
- A line-segment has a definite length. But a line does not have definite length.
Question 4: Write two key differences between a line and a ray.
Answer:
- A line goes without end in both directions but a ray has one endpoint and goes without end in one direction.
- The line AB is same as the line BA. But the ray AB is different than the ray BA.
Question 5: What do collinear points mean?
Answer: Collinear points are points on the same line. Three or more points in a plane are said to be collinear if they all lie on the same line.
Exercise
1. Identify the figure below?

- Ray
- Line
- Line Segment
2. Identify the figure below?
![]()
- Ray
- Line
- Line Segment
3. Identify the figure below?
![]()
- Ray
- Line
- Line Segment
4. Which of the following has a defined length?
- Ray
- Line
- Line Segment
True or False
5. The two lines in the figure below are parallel lines

- True
- False
6. The two lines in the figure below are parallel lines
![]()
- True
- False
Fill in the blanks
7. ………………… has a definite length
- Ray
- Line
- Line Segment
8. ………………… has no end points
- Ray
- Line
- Line Segment
9. Which of the following is only one end point?
- Ray
- Line
- Line Segment
10. Which of the following statements is NOT correct?
- An unlimited number of lines can be drawn passing through a point.
- Two lines always meet at some point.
- A line is longer than a line-segment.
Nice, but exercise may be with answers help us instantly
PQ is represents a
It really Helps it is also very fun!
very nicely articulated
I have to try it
The intersection of three planes can be a line is that true
or false
that doesn’t make sense
It good
I concur 🙂
It really helps!
it was a lot of help
True
Great,love it.But I think you should more questions than that though.
hell na
My Question is : State Whether the following Statement is True or False : 1. A line cannot be Drawn on A Piece of Paper. I Want The Answer WITH EXPLANATION
The answer to the question is false. The reason why is because, according to a textbook that I have been reading, a line is a two-dimensional object that can rest upon any flat object, which means that a line can, in fact, be drawn on a piece of paper. Therefore, the, answer to your problem is false. I hope that this comes to be of great help to you, and the problem you are trying to figure out.
You be looking like horse.
Its a good and helpful information.
This was a really good learning site for rays , line segments and lines Thank You your supporter
Hailee
This is really helpful 🙂
This is really helpful 🙂 Thank you so much. I am in 8th grade so it helps a lot. Thanks once again!!!
How many points can you mark between two given points A and B
I need to know about how to make a starting ray by C
Help me!!!
cool very cool
explain all of thisPoint
Point is the basic building block of Geometry. Every shape is made through the combining the points.
A small dot marked by a pencil is a point. A point has no length or width. It has no thickness. Point is a mark of position. A point specifies the exact location. Point is denoted by a dot (.) and is named by an alphabet.
point
In the figure above, O is a point as it has a definite mark. Here it indicates this point O is located at the centre of the plane. In the figure below, there is another point A. It is located at right bottom of the plan.
point-a
Ray
Let us think of a torch. The light rays come out of it and move away. Let us take example of sun. The rays start from sun and go in all directions and reach to us.
In Geometry also, a ray starts from a point and may go to infinity. It has staring point but has no end point. We say a ray has one endpoint and goes without end in one direction.
ray
In the figure above, the starts from A and the arrow denotes it can go to infinity.
Its length cannot be measured. An unlimited number of rays can be drawn in different directions from a given point
The rays coming from torch or sun are examples of rays.
This is a ray because a ray has one endpoint and goes without end in one direction
Line
line
Look at the figure above. There are arrows on both sides. It indicates it can go further on both sides without end. This is called line.
A line goes without end in both directions. Both ends of a line can go to infinity. A line has no end points. The length of a line cannot be measured. A line has no definite length.
A line is named by any two points on it and written as line AB or line PQ. One and only one line can be drawn passing through two given points A and B. This line is called AB. It may also be called BA. Line BA is the same as line AB. Both pass through the same two points A and B.
An unlimited number of lines can be drawn passing through a given point A.
A horizontal line goes straight left or right across. A vertical line goes straight up or down.
A diagonal line can be in any direction between horizontal line and vertical line.
Line Segment
line-segment
Now look at the figure above. There is no arrow on any end. It starts from one point and ends at another point. This is called a line segment. A section of a line is a line segment.
A line segment has two endpoints. A line segment is a straight line that connects two points. It is the shortest path between the two points. A line segment has definite length. Its length can be measured.
Let us mark two small dots (.) by a pencil as points A and B. Let us join them by drawing a straight line. This forms a line segment. A line segment is named by its two endpoints and written as line-segment AB or line-segment PQ.
line-segment-AB
In the figure above, a line segment AB has two end points A and B. It starts from point A and ends at point B. One and only one line-segment can be between two given points A and B. This line-segment is called AB. It may also be called BA. Line BA is the same as line AB. Both pass through the same two points A and B.
Line segment can also be a part of a line as in the figure below.
line-segment-line
A line-segment may be also a part of ray. In the figure below, a line segment AB has two end points A and B. It is a part of a ray starting from A.
line-segment-ray
Parallel lines
Two lines in the same plane either meet or do not meet. If the two lines on a plane meet, we say the two lines intersect and the point where they meet is called point of intersection. If the two lines cannot meet at any point, they are called parallel lines. No two points can be common to two parallel lines.
parallel-lines
In the figure above, the two lines do not intersect each other. Even if we extend these lines further, they will not touch or meet each other. They are parallel lines.
Intersecting lines
intersecting-lines
Let us look at the two lines AB and CD in figure above. They intersect at point O. Hence they are not parallel lines. Point O is the point of their intersection.
Concurrent lines
Three or more lines passing through the same point on a plane are called concurrent lines. In the figure below, the three lines AB, CD and EF intersect each other at point O.
concurrent-lines
Collinear points
Three or more points in a plane* are said to be collinear if they all lie on the same line.
colinear-points
In the figure above, points A, B and C are on the same line. Hence these three points A, B and C is collinear.
*Flat surface is called a plane in Geometry. We can say a piece of paper from our Exercise Book is a plane.
Measurement of line segment
A ruler is an instrument used in geometry. We use a ruler to draw a line segment. We use it also to measure length of a line segment.
ruler
A ruler is generally 1 ft (30 cm) long and is called One foot ruler. Sometime it is simply called scale. Some rulers are six inches (15cm) long and are called half foot ruler. One edge of a ruler has scales marked in inches and the other edge has scales marked in cm.
We place the ruler with its edge along the line-segment AB with the zero mark of the ruler at the start point A of the line-segment. We read the mark on the ruler at the other endpoint B of the line-segment.
Points to Remember
A small dot marked is a point.
A point has no length, width or thickness.
A point specifies the exact location.
A ray starts from a point and goes to infinity.
A line has no end points.
A line segment has two endpoints.
A line segment connects both endpoints.
If the two lines cannot meet at any point, they are called parallel lines.
Three or more points on the same line are said to be collinear points
A ruler is used to draw a line segment and measure its length.
Questions and Answers
Question 1: Draw two points A and B on a paper and draw line-segment.
Answer: We mark a Point A on a writing page and then mark another point B on the same Page. We join these two points using a line. This is the line segment.
line-segment-AB
Question 2: Draw two intersecting lines.
Answer: We take a ruler and draw a line AB. Then we slightly turn the ruler and draw another line CD in such a way that it passes through any one point of line AB.
intersecting-lines
Question 3: Write two main differences between line and line segment.
Answer:
A line segment has two endpoints. A line has no end point.
A line-segment has a definite length. But a line does not have definite length.
Question 4: Write two key differences between a line and a ray.
Answer:
A line goes without end in both directions but a ray has one endpoint and goes without end in one direction.
The line AB is same as the line BA. But the ray AB is different than the ray BA.
Question 5: What do collinear points mean?
Answer: Collinear points are points on the same line. Three or more points in a plane are said to be collinear if they all lie on the same line.
Exercise
1. Identify the figure below?
line
Ray
Line
Line Segment
2. Identify the figure below?
line-segment-ray
Ray
Line
Line Segment
3. Identify the figure below?
line-segment
Ray
Line
Line Segment
4. Which of the following has a defined length?
Ray
Line
Line Segment
True or False
5. The two lines in the figure below are parallel lines
question5
True
False
6. The two lines in the figure below are parallel lines
parallel-lines
True
False
Fill in the blanks
7. ………………… has a definite length
Ray
Line
Line Segment
8. ………………… has no end points
Ray
Line
Line Segment
9. Which of the following is only one end point?
Ray
Line
Line Segment
10. Which of the following statements is NOT correct?
An unlimited number of lines can be drawn passing through a point.
Two lines always meet at some point.
A line is longer than a line-segment. cause I dont get it
@Rosy I have the same problem and I need explanation too but nobody answer THATS THE PROBLEm
what’s the problem, I may know the answer.
Awesome! This was really helpful.
Nice but exercise must be done with ourselves