Understanding Angles and its Types

Angle is a basic figure in Geometry and looks like this.

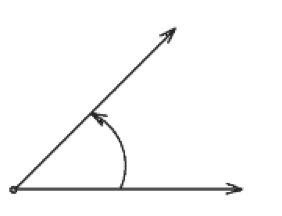
An angle is a figure formed by two rays meeting at a common point. Symbol for an angle is ∠. The common point is called its vertex of the angle. Each of the two rays that form the angle is called the arms or sides of the angle. Thus an angle has three parts one vertex and two sides.

An angle is generally named by three consecutive alphabets such as A, B and C or X, Y and Z. An angle formed by rays AB and BC at vertex B is denoted by ∠ABC.

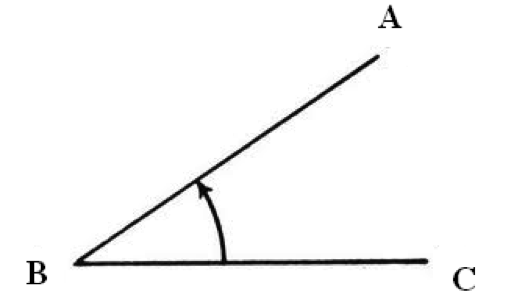
Look at the figure above. The angle formed at the vertex B by the two rays AB and BC is called ∠ABC. This may be also simply called angle B and written in short form as ∠B.  We may notice that B appears in the middle of ABC to denote that this is angle at vertex B.

Think of the two hands of a clock at 12 o’clock. Both hands are at the same point in figure 1.

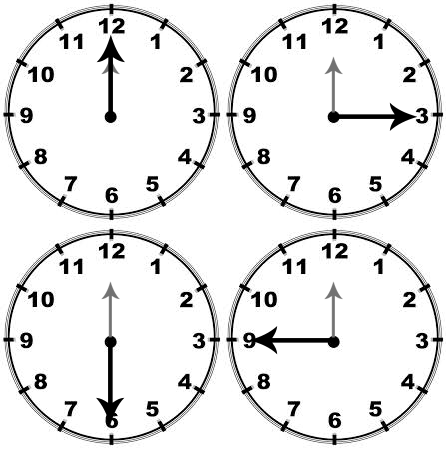
Now the minute-hand starts moving and an angle is formed between the two hands. This goes on increasing with time. One complete rotation makes a circle and forms the maximum angle. An angle measures the amount of turn.

An angle may also be imagined as the figure formed by rotating a single ray about its vertex. The size of an angle depends on the extent of rotation. This gives a measure of the angle. The magnitude of the angle is the amount of rotation of one arm about the vertex to reach to the position of the second arm.

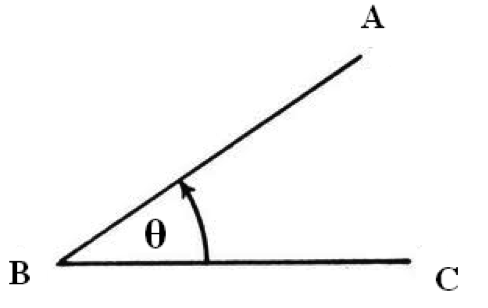
The angle measures the amount of turn between the two arms two and is usually measured in degrees or radians. Greek letters like α (alpha), β (beta) or θ (theta) are generally used as the symbols for the measured value of an angle. It is denoted by ∠θ.

The standard unit of measuring an angle is degree. It is denoted by °. Thus, 30 degree and 60 degree are written as 30° and 60° respectively.

In the above example of clock, the two hands initially make smallest angle 0° and on one complete rotation by the minute hand, the two hands make maximum angle and is named as the angle 360 degree or 360°. The angles in a complete turn add up to 360 degrees. If one complete rotation is divided into 360 equal parts, the measure of each such part is one degree or 1°. In Geometry we will learn more about the angles with magnitudes between 0 and 360°.

Types of Angles

Angles may be classified based on their angle magnitude.

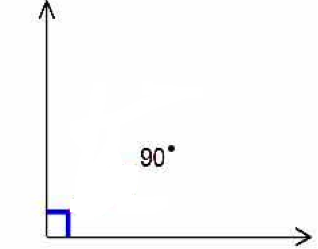
1. Right Angle:

An angle whose measure is equal to 90° is called a right angle. A right angle is formed when two sides make 900. A full rotation consists of four right angles.

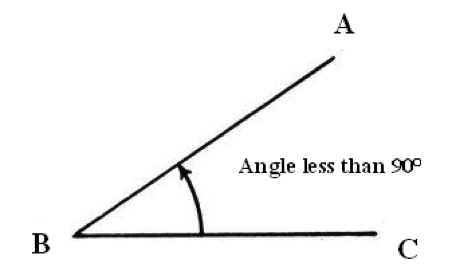
2. Acute angle:

An angle that is less than 90 degrees is called an acute angle.

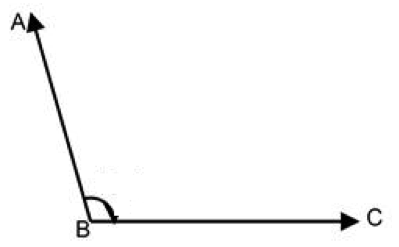
3. Obtuse angle

An angle that is between 90 and 180 degrees is called an obtuse angle.

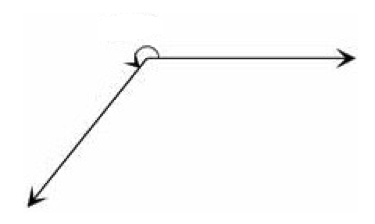
4. Reflex angle

An angle that is greater than 180 degrees is called a reflex angle.

5. Straight angle

A straight angle is an internal angle which is equal to 180°

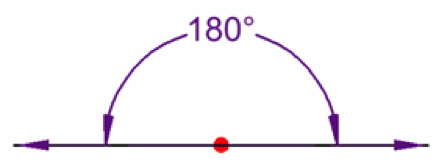
6. Complete Angle

The angles in a complete turn add up to 360 degrees.

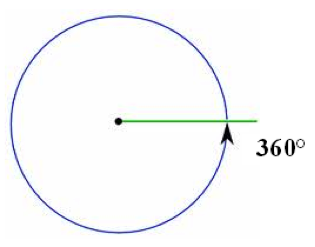
Measuring Angles

A protractor is used to measure angle. It is also called semi-circular protractor. The diagram below shows a protractor.

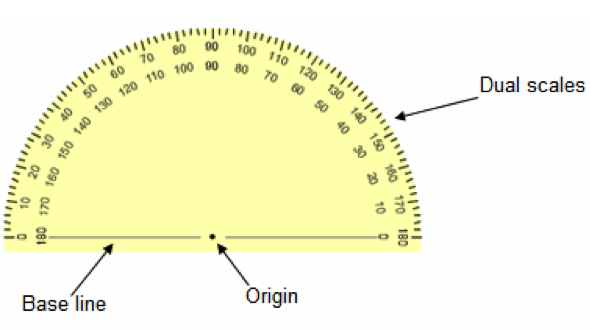
A protractor has dual scales. Each scale is marked in degrees from 0 to 180. Outer scale is marked in degrees from 0 to 180 from left to right. Inner scale is also marked in degrees from 0 to 180 but from right to left. It has a base line at the bottom. The origin is at the centre.

Let us measure an angle with the help of a protractor.

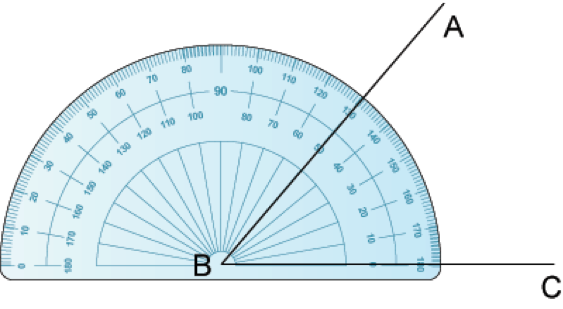
When measuring an angle, the centre of the protractor is placed over the vertex (corner) B of the angle and the base line of the protractor is placed along one of the lines of the angle BC. We look at the position of the second line of the angle BA. Now we read the value on the inner scale for the position of line BA. This is 50°. This is the measurement of ∠ABC. Thus ∠ABC = 50°.

Paired Angles

1. Adjacent angles

Two angles that share the same vertex and one side are called adjacent angle. Adjacent angles are two angles that are side by side and share a common ray. They have a common vertex. Any angle can have adjacent angles on its both sides.

2. Vertically opposite angles

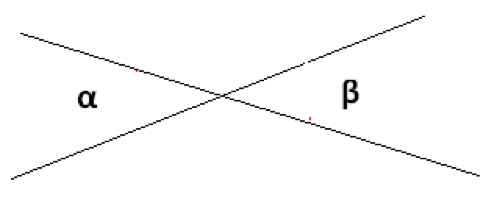
Two angles that have a common vertex and opposite to each other formed by the same two lines are called vertically opposite angles. The two vertically opposite angles are always equal. In the diagram below the two angles α (alpha), and β (beta) are vertical angles and α = β

Complementary and Supplementary Angles

1. Complementary Angles

Two angles whose sum add to 90 degrees are called Complementary Angles.

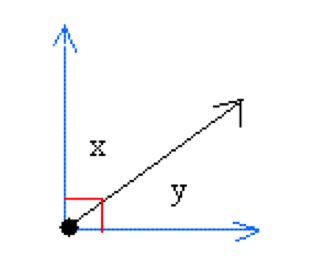
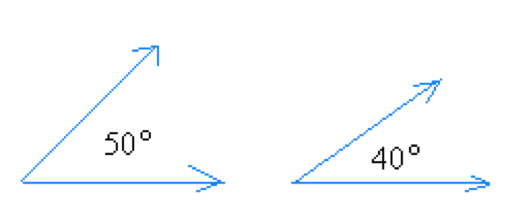
The two complementary angles not necessarily need to be adjacent angles. The following angles are also complementary as the sum of their measures is equal 90 degrees

2. Supplementary Angles

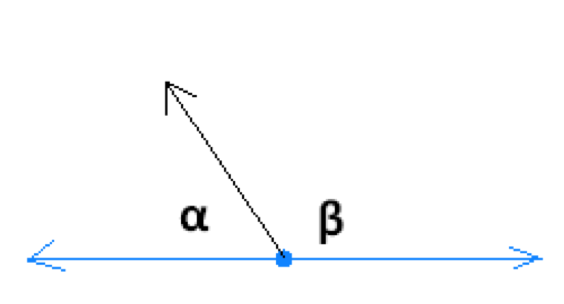
Two angles whose measures add to 180 degrees are called Supplementary Angles. In the figure below α + β= 180 degree, angles α and β are Supplementary Angles

The two supplementary angles need not necessarily be adjacent angles. The following angles are also supplementary as the sum of their measures is equal 180 degrees.

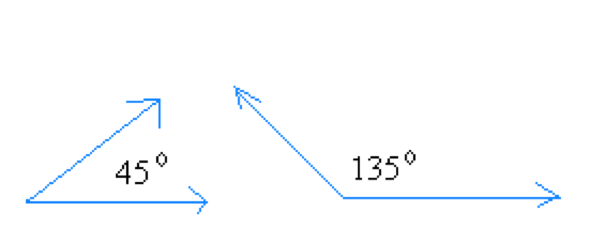
Interior Angle and Exterior Angle

In the figure below, ABC is a geometrical shape called Triangle (we will know more about triangle in other article). Line BC has been extended as line CD. An Interior Angle is an angle inside the shape ABC. The Exterior Angle is the angle between a side of a shape AC, and the extended line CD.

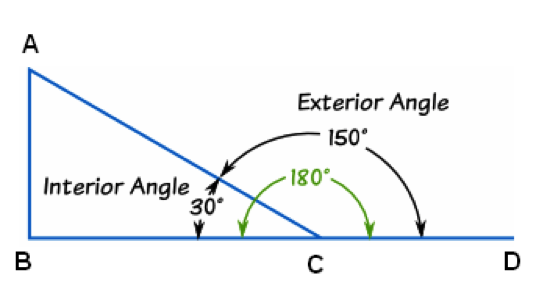
The sum of the Interior Angle and the Exterior Angle are 180°. The two angles are supplementary angles. Here they are adjacent angles also.

Points to Remember

1. A right angle is 90°
2. The standard unit of measuring an angle is degree. It is denoted by °.
3. An acute angle less than 90 degrees.
4. An obtuse angle is more than 90 but less than 180 degrees.
5. A reflex angle is greater than 180 degrees.
6. A straight angle is equal to 180°
7. A complete circular turn makes 360 degrees.
8. A protractor is an instrument to measure angle
9. Two angles that share the same vertex and one side are called adjacent angle.
10. Two angles that have a common vertex and opposite to each other formed by the same two lines are called vertically opposite angles.
11. The two vertically opposite angles are equal.
12. Two angles whose sum is  90 degrees are called Complementary Angles
13. Two angles whose sum is  180 degrees are called Supplementary Angles
14. An Interior Angle is an angle formed inside a geometric shape.
15. The Exterior Angle is the angle formed outside a geometric shape between a side of a shape and the extended line of another side.

Questions and Answers

Question 1: Identify ∠ACB

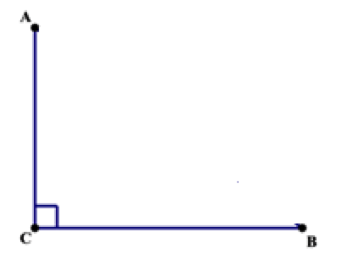
Solution: It is a right angle and measures 90°

Question 2: Look at the figure below and find ∠ACD

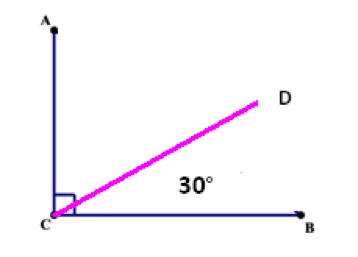
Solution:

∠ACB is a right angle
Hence ∠ACD and ∠DCB are complementary angles.
∠ACD +∠DCB = 90°
∠ACD +30° = 90°
Hence ∠ACD = 60°

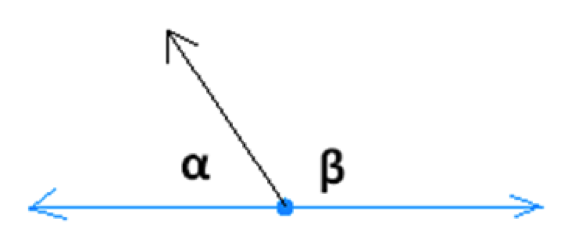
Question 3: Look at the figure below. If ∠β =120°, find value of ∠α.

Solution:

Angles α and β are Supplementary Angles.
Hence α + β= 180 degree,
As ∠β =120°, ∠ α = 180-120 = 60°

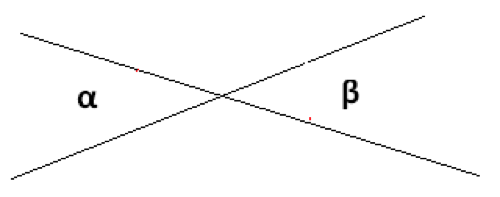
Question 4: Look at the figure below. If ∠α =30°, find value of ∠β.

Solution:

The two angles α (alpha), and β (beta) are vertically opposite angles and so α = β

As α is 30°, so β is also equal to 30°

Question 5: Find the complement of angle 45°

Solution:

Sum of two complement angles are 90°. As one angle is 45°, the other angle = 90-45= 45°

Exercise:

1. ∠ABC is 225°. It is a/an

1. Acute angle
2. Obtuse angle
3. Reflex angle

2. The measurement of a straight angle is

1. 90°
2. 180°
3. 360°

2. What is value of the supplementary angle of an angle measuring 75°?

1. 15°
2. 75°
3. 105°

4. Find the value of the complementary angle of an angle measuring 30°

1. 30°
2. 60°
3. 150°

5. What is measure of a right angle?

1. 0°
2. 90°
3. 180°

True Or False

6. Two vertically opposite angles are always equal.

1. True
2. False

7. The sum of the Interior Angle and the Exterior Angle are 360°.

1. True
2. False

Fill in the blank

8. The measure of …………. is 360°

1. Right angle
2. Obtuse angle
3. Complete angle

9. One complete rotation of minute hand in one hour makes angle of ……. degree

1. 90°
2. 180°
3. 360°

10. Which of the following statements is NOT correct?

1. Two complementary angles are not necessarily adjacent angles
2. Two adjacent angles are always supplementary
3. The two vertically opposite angles cannot be adjacent angles