Trigonometric Functions: An angle having measure greater than but less than
is called an acute angle. Consider a right angled triangle ABC with right angle at B. The side which is opposite to right angle is known as hypotenuse, the side opposite to angle A is called perpendicular for angle A and the side opposite to third angle is called base for angle A.
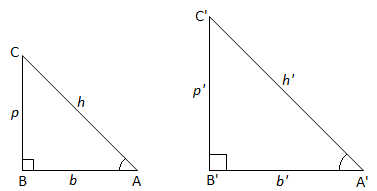
Any ratio of two of the sides depends only on the measure of angle A, for if we take a lager or smaller right angle A’ B’ C’ with A = A’ then
, (as these triangles are similar)
Thus any ratio of the lengths of two sides of the triangle is completely determined by angle A alone and is independent of the size of the triangle. There are six possible ratios that can be formed from the three sides of a right angled triangle. Each of them has been given a name as follows.
Definitions:
The abbreviations stand for sine, cosine, tangent, cotangent, secant and cosecant of A respectively. These functions of angle A are called trigonometrical functions or trigonometrical ratios.
Trigonometrical functions of any angle: Let A be a given angle with specified initial ray. We introduce rectangular coordinate system in the plane with the vertex of angle A as the origin and the initial ray of angle A as the positive ray of the x-axis. We choose any point P on the terminal ray of angle A. Let the coordinates of P be (x, y) and its distance from the origin be r, then we define
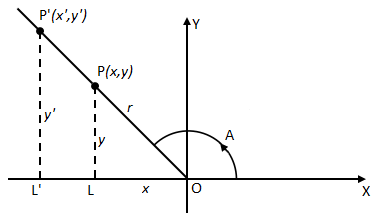
These quantities are functions of the angle A alone. They do not dependon the choice of the point P and the terminal ray for if we choose a different point P’ (x‘, y‘) on the terminal ray of A at a distance r‘ from the origin, it is clear that x‘ and y‘ will have the same sign as those of x and y respectively and because of similar and
,
,
,
, etc. will be equal to
,
,
, respectively (r being always positive).
Also any trigonometrical function of an angle is equal to the same trigonometrical function of any angle
, where n is any integer since all these angles will have the same terminal ray.
For example, . After the coordinates system has been introduced, the plane is divided into four quadrants. An angle is said to be in that quadrant in which its terminal ray lies. For positive acute angles this definition gives the same result as in case of a right angled triangles since x and y are both positive for any point in the first quadrant and consequently are the length of base and perpendicular of the angle A.
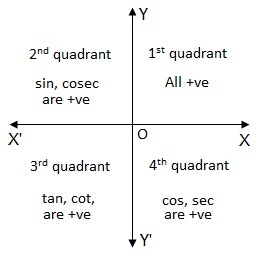
- In 1st quadrant
,
,
,
,
,
are all positive as x, y are positive.
- In 2nd quadrant x is negative and y is positive therefore, only
and
are positive.
- In 3rd quadrant both x and y are negative, therefore only
and
are positive.
- In 4th quadrant x is positive and y is negative, therefore only
and
are positive.
Limits of the values of trigonometrical functions:
and
therefore,
Relation between the trigonometrical ratios of angles: Let O be the vertex of an angle A, OX its initial ray and OP its terminal ray. Let P (x, y) be a point on the terminal ray.
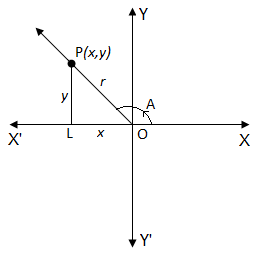
Let PL be perpendicular to OX’. Let OP = r then
Now,
I.
Proof:
II.
Proof:
III.
Proof:
IV.
Proof:
similarly, and
Important Results
;
;
;
;
;
Note: Positive or negative sign before the root depends on the quadrant in which A lies.
Examples:
Ex. – 1. Prove that
Sol. – L.H.S.
R.H.S.
Ex. – 2. If
. Then prove that the value of each side is
Sol. – Let
…(i)
then,
…(ii)
Multiplying (i) and (ii) we get
or, Hence each side
Ex. – 3. If , prove that
Sol. – Given,
Now, L.H.S.
R.H.S.
Exercise:
Prove the following trigonometrical identities.
1. .
2. .
3. .
4. .
5. .
6. .
7. If , prove that
.
8. If , prove that
.
9. If then prove that the value of each
.
10. If , find the value of
,
,
. Porvided
.
11. If ,
, find
,
and
.
12. If , find
.
P.S. – Please find the answers here.
Nice page. I like your proofs. I needed a quick review on these topics and this page helped me remember what I needed to remember.