Understanding Trigonometric Ratios of Angles in Each Quadrant

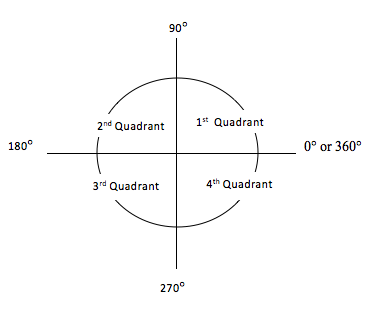
xy plane is divided into four equal positions known as quadrants. The quadrants are numbered in the counter clockwise direction.

The x and y axis intersects at a point. Since angles at a point add up to 360°, each quadrant is equivalent to an angular measure of 90°. Dividing 360° into 4 equal parts and labeling the axis in counter clockwise direction, we get that the positive x axis is equivalent to 0° or 360°. The positive y axis is equivalent to 90°, the negative x axis is equivalent to 180° and the negative y axis is equivalent to 270°.

A unit circle is a circle whose radius is one unit. The center of the circle may be positioned on any point on the xy plane. In our case, we will consider a unit circle whose center is the origin. The diagram below shows the parts of a unit circle.

Unit Circle

Trigonometric ratios of angles in the first quadrant, between 0° and 90°

Consider following triangles DOA and COB where their internal angles at O are 60° and 45° respectively. The scale of the drawing is 10 small units represent 1 bigger unit, the radius of the circle.

Note that OC = OD = radius of circle = 1

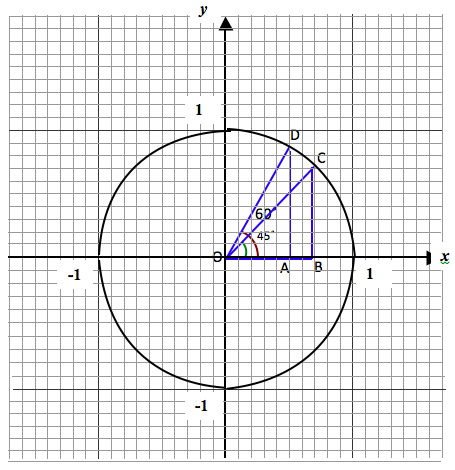
In triangle DOA, taking angle DOA = 60°, Scale of the drawing is 10 small units represent 1 bigger unit,

The opposite side AD = 8.5 small units or 0.85 of a bigger unit.

Opposite side = AD = 0.85

The adjacent side OA = 5 small units or 0.5 of a bigger unit.

Adjacent side = OA = 0.5

The hypotenuse OD is equal to radius of circle = 10 small units = 1 bigger unit.

Hypotenuse = OD = 1

We then approximate the trigonometric ratios,

$\cos 60 ^{\circ} = \dfrac{OA}{OD} = \dfrac{0.5}{1} = 0.5$

$\sin 60 ^{\circ} = \dfrac{AD}{OD} = \dfrac{0.85}{1} = 0.85$

$\tan 60 ^{\circ} = \dfrac{AD}{OA} = \dfrac{0.85}{0.5} = 1.7$

In triangle OBC, taking angle COB = 45°,

The opposite side BC = 7 small units = 0.7 of a bigger unit

Opposite side = BC = 0.7

The adjacent side OB = 7 small units = 0.7 of a bigger unit

Adjacent side = OB = 0.7

The hypotenuse OC = 10 small units = 1 bigger unit

Hypotenuse = OC = 1

We then approximate the trigonometric ratios,

$\cos 45 ^{\circ} = \dfrac{OB}{OC} = \dfrac{0.7}{1} = 0.7$

$\sin 45 ^{\circ} = \dfrac{BC}{OC} = \dfrac{0.7}{1} = 0.7$

$\tan 45 ^{\circ} = \dfrac{BC}{OB} = \dfrac{0.7}{0.7} = 1$

It can be confirmed from tables that these are correct approximations.

Point to note here is that all the trigonometric ratios are positive in the first quadrant.

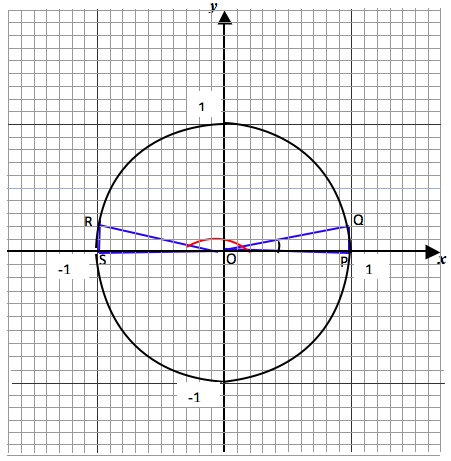
Trigonometric ratios of angles in the second quadrant, between 90° and 180°

Consider the following diagram

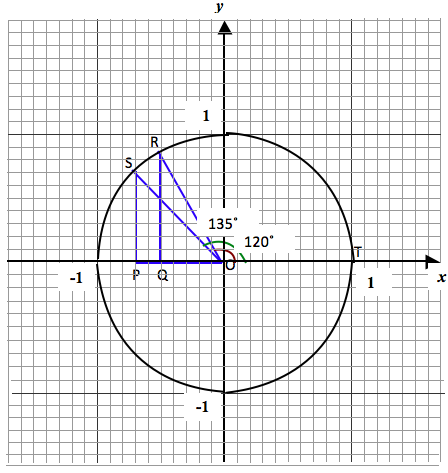
The exteriors angles of triangles POS and QOR are 135° and 120° degree.

To determine their trigonometric ratios, we find the trigonometric ratios of their supplement angle while taking into account the positive or negative distance of a point from the origin.

The supplement of angle SOT = 135° is angle POS = 180 – 135 = 45°.

We therefore, define the opposite, adjacent side and hypotenuse of angle 135° with reference to angle 45° in the second quadrant (in triangle POS).

In triangle POS, taking angle POS = 45°,

Opposite side = PS = 7/10 = 0.7 (positive side of y axis)

Adjacent side = OP = -7/10 = -0.7 (negative side of x axis)

Hypotenuse = OS = 1 (radius as positive)

We then approximate the trigonometric ratios in the second quadrant

$\cos 135 ^{\circ} = \dfrac{OP}{OS} = \dfrac{-0.7}{1} = -0.7$

$\sin 135 ^{\circ} = \dfrac{PS}{OS} = \dfrac{0.7}{1} = 0.7$

$\tan 135 ^{\circ} = \dfrac{PS}{OP} = \dfrac{0.7}{-0.7} = -1$

The supplement of angle ROT = 120° is angle ROQ = 180 – 120 = 60°.

We also define the opposite, adjacent side and hypotenuse of angle 120° with reference to angle 60° in the second quadrant (in triangle ROQ).

In triangle ROQ, taking angle ROQ = 60°, the opposite side = RQ = 0.85 (positive side of y axis)

Adjacent side = OQ = -5/10 = -0.5 (negative side of x axis)

Hypotenuse = OR = 1 (take radius to be positive)

We then approximate the trigonometric ratios in the second quadrant

$\cos 120 ^{\circ} = \dfrac{OQ}{OR} = \dfrac{-0.5}{1} = -0.5$

$\sin 120 ^{\circ} = \dfrac{RQ}{OR} = \dfrac{0.85}{1} = 0.85$

$\tan 120 ^{\circ} = \dfrac{RQ}{OQ} = \dfrac{0.85}{-0.5} = -1.7$

It can be confirmed from tables that these are better approximations.

We see that the cosine and tangent are negative in second quadrant while the sine is positive. It is also important to note that the magnitude of the ratios does not change from the first quadrant.

Therefore, we can make an important remark that

The sine of an angle in the second quadrant is positive and equal to the sine of the same angle in the first quadrant.
The cosine and tangent of an angle in the second quadrant is negative and equal in magnitude but opposite in sign to the cosine and tangent, respectively, of the same angle in the first quadrant.

Symbolically, let y be the angle in the first quadrant then

$\cos y = -\cos (180 - y)$

$\tan y = -\tan (180 - y)$

$\sin y = \sin (180 - y)$

Trigonometric ratios of angles in the third quadrant, between 180° and 270°

Consider the following diagram

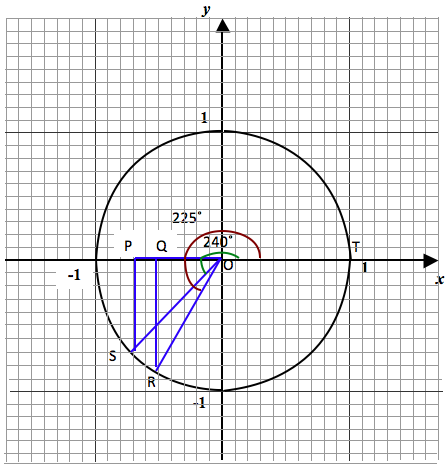
To determine the trigonometric ratios of angles 240° and 225°, we find the trigonometric ratios of the equivalent angles measured in the counterclockwise direction from negative x axis (180° axis), that is, 240° – 180° = 60° and 225° – 180° = 45° respectively, while taking into account the positive or negative distance of a point from the origin.

We therefore, define the opposite, adjacent side and hypotenuse of angle 240° with reference to angle 60° in the third quadrant (in triangle ROQ). In triangle ROQ, taking angle ROQ = 60°.

Opposite side = RQ = -8.5/10 = -0.85 (negative direction of y axis)

Adjacent side = OQ = -5/10 = -0.5 (negative side of x axis)

Hypotenuse = OR = 1 (take radius to be positive)

We then approximate the trigonometric ratios in the third quadrant

$\cos 240 ^{\circ} = \dfrac{OQ}{OR} = \dfrac{-0.5}{1} = -0.5$

$\sin 240 ^{\circ} = \dfrac{RQ}{OR} = \dfrac{-0.85}{1} = -0.85$

$\tan 240 ^{\circ} = \dfrac{RQ}{OQ} = \dfrac{-0.85}{-0.5} = 1.7$

We also define the opposite, adjacent side and hypotenuse of angle 225° with reference to angle 45° in the third quadrant (in triangle POS).

In triangle POS, taking angle POS = 45°,

Opposite side = PS = (-7)/10 = -0.7 (negative side of y axis)

Adjacent side = OP = (-7)/10 = -0.7 (negative side of x axis)

Hypotenuse = OS = 1 (take radius to be positive)

We then approximate the trigonometric ratios in the third quadrant

$\cos 225 ^{\circ} = \dfrac{OP}{OS} = \dfrac{-0.7}{1} = -0.7$

$\sin 225 ^{\circ} = \dfrac{PS}{OS} = \dfrac{-0.7}{1} = -0.7$

$\tan 225 ^{\circ} = \dfrac{PS}{OP} = \dfrac{-0.7}{-0.7} = 1$

Therefore, we can make an important remark that

The tangent of an angle in the third quadrant is positive and equal to the tangent of the same angle in the first quadrant.
The cosine and sine of an angle in the third quadrant is negative and equal in magnitude, but opposite in sign, to the cosine and sine, respectively, of the same angle in the first quadrant.

Symbolically, let y be the angle in the first quadrant then

$\cos y = - \cos(y-180)$

$\tan y = \tan(y-180)$

$\sin y = - \sin(y-180)$

Trigonometric ratios of angles in the fourth quadrant, between 270° and 360°

Using the same argument as discussed above, we have the following

The cosine of an angle between 270° and 360° is positive, while sine and tangent are negative.

If y is such an angle, then

$\cos y = \cos(360 - y)$

$\tan y = - \tan(360 - y)$

$\sin y = - \sin(360 - y)$

Trigonometric ratios of negative angles

A negative angle implies that an angle is measured from 0° to the clockwise direction of the reference point.

If the angle is -50°, then it is 50° in the clockwise direction of 0°.

This angle is equivalent to 360 – 50 = 310°.This angle is in the fourth quadrant. If we are asked to find the sine of this angle, this would be the procedure;

$\sin (-50 ^{\circ}) = \sin (310 ^{\circ}) = - \sin (360 - 310) = - \sin 50 ^{\circ}$

Because sine is negative in the fourth quadrant

From trigonometric tables, sin 50° = 0.766

sin (-50) = – sin 50° = -0.766

Simplify sin -175.

-175° = 360 – 175 = 185°

185° is in the third quadrant; hence, its sine will be negative

sin -175° = sin 185 =- sin (185 – 180) =- sin 5 = -0.08716

Trigonometric ratios of angles more than 360°

An angle that is more than 360° implies that an object underwent a rotation that is more than one cycle about a fixed point. To determine the basic trigonometric ratio of such angle, we subtract a suitable positive multiple of 360° till the angle is positive and less than 360°. Thereafter, we apply the appropriate procedure to determine its trigonometric ratio in question.

Find the cosine of 549°.

cos 549° = cos (549° – 360°) = cos189°

189° is in the third quadrant, hence it is negative.

cos 189° = – cos(189° – 180°) = – cos 9 = -0.9877

Find the sine of 850°.

sin 850° = sin (850° – 360°- 360°) = sin 130°

130° is in the second quadrant; hence its sine is positive

sin 130° = sin (180° – 130°) = -sin 50° = -0.766

Trigonometric ratios of 0°, 90°, 180° and 270°

Angle 0°

Consider triangle OPQ, with respect to angle QOP, OP is the adjacent, OQ the hypotenuse and QP the opposite side.

As angle QOP decreases, QP becomes smaller and smaller and OP becomes bigger and bigger. When angle QOP is zero, OP and OQ become equal and on the same line and QP becomes zero.

When angle QOP = 0°, opposite side QP = 0 units, adjacent side OP = hypotenuse OQ = 1

$\therefore \sin 0 = \dfrac{0}{1} = 0$ ,

$\cos 0 = \dfrac{1}{1} = 1$ ,

$\tan 0 = \dfrac{0}{1} = 0$ ,

Angle 180°

Consider triangle OSR, with respect to angle SOR, OS is the adjacent, OR the hypotenuse and SR the opposite side.

To find the trigonometric ratio of ROP, we find the trigonometric ratios of angle SOR while considering the distance of a point to the positive or negative point of the origin.

As angle SOR decreases, SR becomes smaller and smaller and OS becomes bigger and bigger. When angle SOR is zero, OS and OR become equal and on the same line, and SR becomes zero.

Thus, when angle SOR = 0°, angle ROP = 180°, opposite side, SR = 0 units, adjacent side, OS = hypotenuse, OR = -1

Taking the hypotenuse, the radius of the circle to be zero, we have the following

$\therefore \sin 180 ^{\circ} = \dfrac{0}{1} = 0$ ,

$\cos 180 ^{\circ} = \dfrac{-1}{1} = -1$ ,

$\tan 180 ^{\circ} = \dfrac{0}{-1} = 0$ ,

Angle 90° and 270°

Using the same argument for angles 90° and 270°, we have the following results

$\therefore \sin 90 = 1$ $\cos 90 = 0$ $\tan 90 = \infty$

$\therefore \sin 270 = -1$ $\cos 270 = 0$ $\tan 270 = \infty$

Summary

All ratios are positive in first quadrant.
Only Cosine is Positive in Fourth Quadrant.
Only Tangent is positives in third quadrant
Only Sine is positive in Second Quadrant.

Graphically

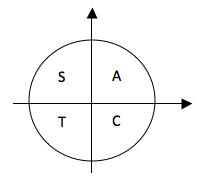
To remember, it is commonly termed as ACTS (reading clockwise direction).

Sin Cos and tan of 0, 90, 180 and 270 are as follows.

$\sin 0 = 0$ $\cos 0 = 1$ $\tan 0 = 0$
$\sin 90 ^{\circ} = 1$ $\cos 90 ^{\circ} = 0$ $\tan 90 ^{\circ} = \infty$
$\sin 180 ^{\circ} = 0$ $\cos 180 ^{\circ} = -1$ $\tan 180 ^{\circ} = 0$
$\sin 270 ^{\circ} = -1$ $\cos 270 ^{\circ} = 0$ $\tan 270 ^{\circ} = \infty$

Symbolically, let y be the angle in the first quadrant then

$\cos y = -\cos (180 - y)$
$\tan y = -\tan (180 - y)$
$\sin y = \sin (180 - y)$
$\cos y = - \cos(y-180)$
$\tan y = \tan(y-180)$
$\sin y = - \sin(y-180)$
$\cos y = \cos(360 - y)$
$\tan y = - \tan(360 - y)$
$\sin y = - \sin(360 - y)$

Exercise

Evaluate the following

Sin 65°
Sin 270° – Cos 0°
Cos 560°
Tan 540°
Cos 315°
Tan 125°
Sin 90° + sin 180°
Cos 450°
Tan 720° + tan (-180°)
Sin (-250°)

Comments

tirupathi says

January 14, 2015 at 8:59 am

sec A=cosecB then findout the value of Tan(A+B)

s.sugumaran says

December 12, 2015 at 2:28 pm

All the Scientists are not intelligent But all the Good Mathematician are intelligents only.

s.sugumaran says

December 12, 2015 at 2:29 pm

All the Scientists are not intelligent But all the Good Mathematician are intelligents only.

Willa says

June 13, 2021 at 1:56 pm

The angles 90°, 180°, 270° lie in what quadrant?

Trigonometric ratios of angles in the first quadrant, between 0° and 90°

Trigonometric ratios of angles in the second quadrant, between 90° and 180°

Trigonometric ratios of angles in the third quadrant, between 180° and 270°

Trigonometric ratios of angles in the fourth quadrant, between 270° and 360°

Trigonometric ratios of negative angles

Trigonometric ratios of angles more than 360°

Trigonometric ratios of 0°, 90°, 180° and 270°

Angle 0°

Angle 180°

Angle 90° and 270°

Summary

Exercise

Comments

Leave a Reply Cancel reply