Solution of triangles is the term for solving the main trigonometric problem of finding the parameters of a triangle that include angle and length of the sides. The triangle can be located either on the plane or a sphere.
Figure 1 indicates a triangle with sides a, b and c and angles A, B and C respectively. A general form triangle has 6 main components. The whole topic is around finding these components of a triangle.
You can have multiple scenarios in solving a triangle, sometimes a particular side is missing and sometimes angles missing. There are different techniques to solve each of these triangles with the help of trigonometric functions. We will discuss each of these examples.
1. Two angles and no side given
If two angles are given, we can find the third angle. Consider the following figure with only angle A and angle B are known to us and we are interested in finding the third angle C.
We know the sum of all angles of a triangle is equal to 180o i.e.
∠A + ∠B + ∠C = 180o
∠C = 180o – (∠A + ∠B)
Example
Figure 2: Two angles with no side given
In the above figure, if ∠A = 89 o and ∠C = 56o, find the value of ∠B.
Solution:
We know the sum of all angles of triangle is 180o.
∠B = 180 o – (∠A + ∠C)
∠B = 180 o – (89 o + 56 o)
∠B = 180 o – (145 o)
∠B = 35 o
2. Two angles and one side / one angle and two sides (not included angle)
See figure 3, given two angles A and B and a side b, the standard method of solving this kind of problem requires us to use fundamental relations.
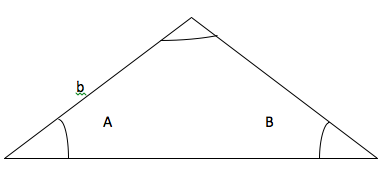
Figure 3: Two angles and one side given
For this scenario we can use law of sine which can be used to find the remaining sides of this triangle. The third angle can be found by the method discussed in the previous topic regarding the sum of all angles of the triangle is equal to 180o.
Law of Sine (or Sine Rule)
Sine law or sine rule is an equation connecting the length of the sides of an arbitrary triangle to the sines of its angle. This is one of the two laws in trigonometry which is commonly used to find the lengths and angles in a general triangle. Consider a figure 1 again.
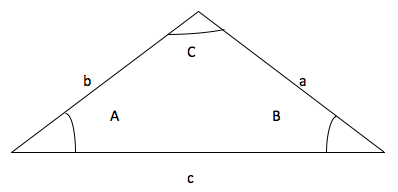
Law of sine states, if you divide the side ‘a’ by the sine of angle ‘A’ it is equal to side ‘b’ divided by sine of an angle ‘B’ and also equals to side ‘c’ divided by the sine of angle ‘C’.
Mathematically it can be written as:
Where a, b and c are the sides and A, B and C are the opposite angles of these sides respectively.
You will see in some references that some authors have stated the sine rule as the reciprocal of the above ratios. Hence, the both forms are true i.e.
From the above equations it is clear that given the any two angles and any side (except the included angle given between the two sides which we will discuss in the next topic), we can find the rest of the components of a triangle. This technique is also called triangulation. For example it is not necessary that the two given angles must be those who opposite sides are known to us. We can find the third angle by using the law: sum of all angles of a triangle = 180 o. After finding this third angle we can apply the sine rule to find other parameters.
Example:
Find the length ‘a’ in figure 1, If ∠A = 40 o, ∠C = 70 o and side c = 5 cm.
Solution:
Using the sine rule we can solve this triangle.
Have a look at the parameters and then apply appropriate equation to find the length a.
Cross multiply.
a = 3.42 cm
3. Two sides and included angle
The sine rule failed in this case because the opposite angles to the given sides are missing. Also an opposite side is missing to which an angle is given. Consider the following figure of the triangle in which the two sides and an included angle is given. From this data we have to solve the triangle.
Cosine Rule
There is another rule called cosine rule according to which we must be aware of the lengths of the two sides let’s say b and c here, and the angle A between these two sides. The side a can be determine from the law of cosines:
Similarly it is true for the other sides too:
After finding the all three sides you can find and angle by re-arranging the above equations or by applying sine rule.
Example:
If the length b = 10 ft, c = 12 ft and the angle A = 70 o in figure 1, find the length a.
Solution:
Given the two sides and an included angle, we must be sure to apply cosine rule here.
Plug in the values, b = 10 ft, c = 12 ft and the angle A = 70o
a = 12.7 ft
4. Three sides and no angle
Let’s see which rule works here. We are given the three sides only and want to solve the triangle i.e. need to find the other 3 angles. Figure 6 is showing this scenario. Let’s see if we can apply the sine rule here.
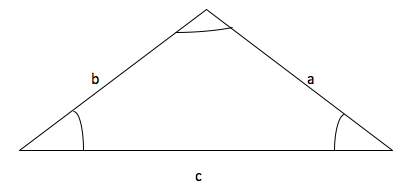
Figure 5: Three sides and no angle given
Suppose we want to find the angle B (see figure 1) and the sides, a, b and c are known to us.
The sine rule is
We can see by plugging in all the given sides in the ratios above, we cannot find the value of angles. We can even get the three equation but we do not have enough data to calculate the value of any angle. Hence, the sine rule failed here as none of the angle is known to us. Let’s apply cosine rule to this problem.
Cosine rule is
Now let us solve this equation for angle B.
Take square on both sides of the above equation.
Re-arrange by bringing the square terms on one side.
$latex 2ac CosB = a^2+c^2-b^2$
Divide both sides by 2ac.
Take inverse of cosine on both sides.
Example:
The three sides of a triangle are given: a = 10cm, b = 8cm, c = 7cm Find the angle C.
We can re-arrange this cosine formula to arrive at our answer. Select an appropriate equation from the above mentioned equations. We need to find the angle C, so we will select:
Insert the given values.
C = 52.62o
In case you need to find the other angles of this triangle, use the law of sines.
Note that we use law of sines in the cases where the angle to be found is smaller comparatively to the other angles because the inverse sine function gives answers less than 90 o even for angles greater than 90 o. Hence, the law of cosines is safer than the law of sines for determining an angle. Also note that the smaller angle is the one which is opposite to the shorter side.
Summary
Think of trigonometry as a tool box. It has the number of useful laws and geometrical methods to solve a particular triangle for any unknowns. The sine rule and the cosine rule are the most important rules.
There are certain steps involve in solving a triangle:
- Draw a diagram if not given. This will help in visualizing things more comfortably.
- See what is known and what is unknown to you.
- Apply the proper formula of sine rule or cosine rule according to the sides or angles given.
- Re-arrange the selected formula where necessary.
- Identify the units of all the parameters (which must be same and if not then apply unit conversion methods).
- Solve the equation once you have passed the above steps.
- Verify your answers once you have calculated them. Angles can be verified by adding all 3 of them, and their sum must be equal to 180 o. If you have find the sides using cosine rule, then the sides can be verified by applying the sine rule to them. If the answers by both rules are similar then you have done a good job.
Exercise
Question 1: If one angle of the triangle is 50 o and the other angle is twice the third angle, find the two unknown angles.
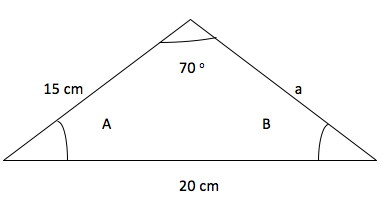
Question 2: Solve the following triangle for side a and angle A and B.
Question 3: Given the following triangle ABC with angle ABC = θ.
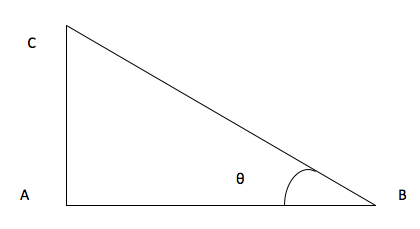
Find using cosine rule, the value of the side CA if length AB = 7cm, length BC = 9cm and angle θ = 60o.
Question 4: Given you the isosceles triangle (which have two sides equal) with length of two sides equal to x and between them is 80 o. Find the third side if it is twice the first two sides.
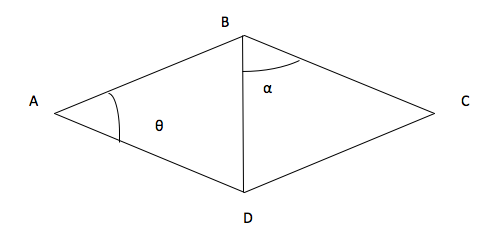
Question 5: Given that the triangles ABD and CBD are similar. Find the angle θ if length AB = BD = 10cm and angle CBD = 45o.
Question 6: A damaged tower is fenced off for safety reasons. To find the distance from the nearest house, a person stands at point P and measure the angle of elevation as 25 o. He then walks 15 meters directly from the house towards the base of the tower till the point Q where the angle of elevation becomes 45o.
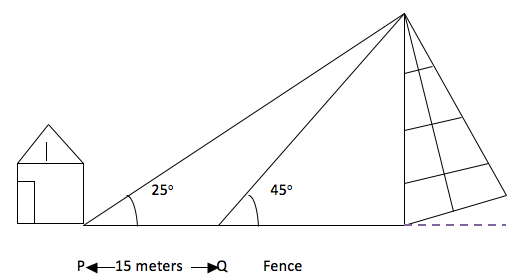
Calculate the distance of house from the tower.
Question 7: Given the cotangent of an angle θ is 0.57. If the initial and terminal side of an angle θ is 20 ft and 30 ft, find the side opposite to an angle θ.
Hi, I think your final example might be wrong:
The three sides of a triangle are given: a = 10cm, b = 8cm, c = 7cm Find the angle C.
Although I am still learning this, I cannot prove your answer of 52.62 degrees.
I calculated C to be: 44.0486 degrees (4 d.p.).
If I am incorrect, please explain why –
I would really like to fully comprehend this.
Many thanks,
Rich C
did u have the answers for the exercises’ question?